Algorithms + Data Structures = Programs

一.导论

1.基本概念和术语

Data 数据
Data Element 数据元素
node节点
Data Ltem 数据项
Data Object数据对象

2数据结构 Data Structure

数据结构包括以下三个部分

数据结构之间的逻辑关系也叫逻辑结构
数据元素关系在计算机内存中的表示也叫数据结构的物理结构或者数据的存储结构
数据的运算和实现 即对数据结构元素可以施加操作也i及在对应存储结构的实现

逻辑结构

3.数据类型

一些基本的数据结构可以用数据类型实现，如数组字符串等
而另一些常用的数据结构如栈队列树图不能直接用数据类型表示

抽象数据类型

可以用DSP三元组表示出来 D是数据对象 S是D上的关系集 P是对D的基本操作集

定义格式

Abstract Data Type 抽象数据类型名{
数据对象
数据关系
基本操作
}Abstract Data Type抽象数据名

基本操作定义格式为
基本操作名（参数表）
初始条件《初始条件描述》
操作结果《操作结果描述》

参数表：赋值参数 职位操作提供输入值
         引入参数&打头 除可提供输入值外 还将返回操作结果

4算法

有穷性确定性可行性输入输出

算法的设计和要求

正确性可读性健壮性高效性（鲁棒性）

5.算法的分析

1.时间效率

算法的时间效率的度量

算法运行时间＝每条语句频度语句执行一次时间

n*n矩阵相乘的算法
for(i=1;i<=n,i++)//n+1次
    for(j=1;j<=n;j++)//n（n+1）
        c[i][j]=0;//n*n
        for(k=0;k<=n;k++)//n*n*（n+1）
            c[i][j]=c[i][j]+a[i][k]*b[k][j];//n*n*n

执行n*n*n
    T（n）为2n^3+3n^2+2n+1

算法时间复杂度的渐进表示法

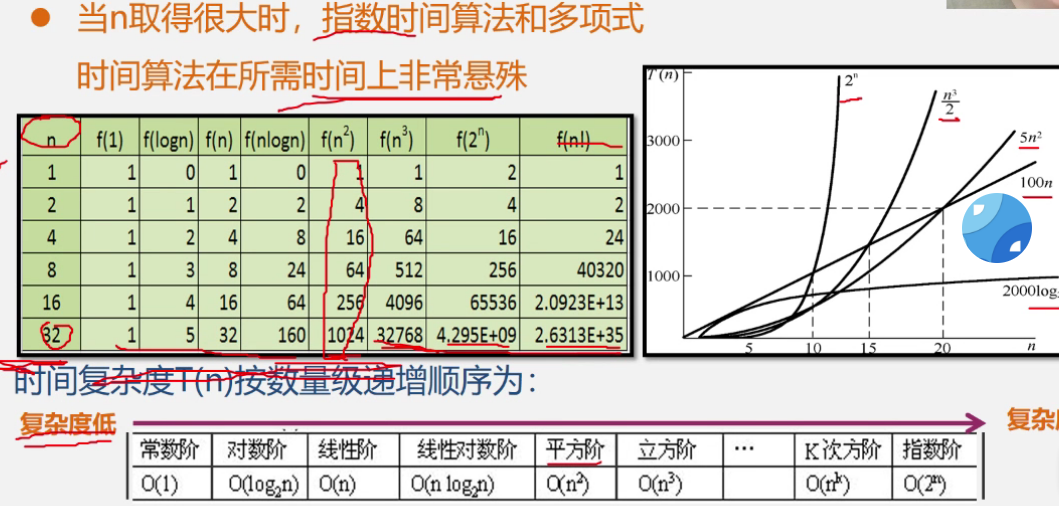
比较算法比较我们仅仅比较数量级

T1(n)=10*n^2和T2(n)=5n3 O 前者好

有一个辅助的f（n）使得当n无限大，T(N)/F(N)极限为不同为零的常熟

则称f（n）是t（n）的同数级函数记作T(n)=O（f(n)）

称O（f(n)）为算法的渐进时间复杂度简称为时间复杂度
F(n)=n^m+nm-1…则T(N)=o(N^M)
算法基本操作次数也和问题输入而不同

比如说
    for(i=0;i<n,i++)
        if(a[i]==e)return i+1;
	return 0;
最好只有一次执行
最坏要执行n次
    
最坏时间复杂度：最坏情况下
最好时间复杂度：最好情况下
平均时间复杂度为O(n)

复杂的算法，可以分成几部分利用O的加乘法则
加法T(n)=T1(n)+T2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))
乘法T(n)=T1(n)xT2(n)=O(f(n))xO(g(n))=O((f(n)xg(n))

2空间复杂度

算法所要的存储空间度量

S（n）=O（f（n））

n为为问题的规模

将一维数组a的n个数逆序放到元素组
for(i=0;i<n/2;i++){
    t=a[i];
    a[i]=a[n-i-1];
    a[n-1-i]=t;
}//空间复杂度为O（1）

for(i=0;i<n;i++)
b[i]=a[n-1-i];
for(i=0;i<n;i++)
    a[i]=b[i];
//空间复杂度为O（n）

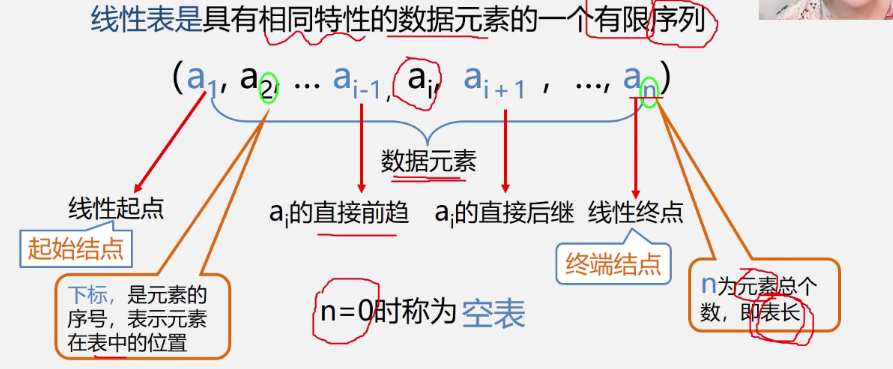
二.线性表linear list

1线性表的定义和特点

例子

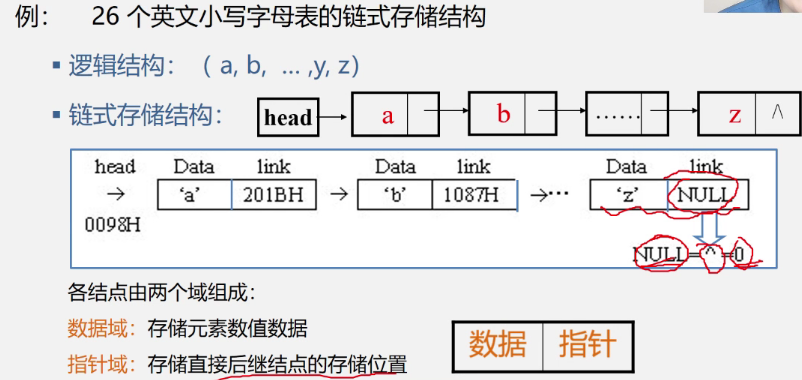
如26英文字母数据元素都是字母为线性

线性表的逻辑特征

在非空中有且仅有一个开始或者终端的结点，他没有前趋而仅有一个后续a2 或者没有后趋，而仅有一个直接前趋an-1

案例引入

一元多项式

2.线性表的类型定义

基本操作

lnitlist（&L）构造一个空的线性表L
DestroyList（&L）初始条件线性表已经有了操作结果摧毁线性表
ClearList（&L）初始条件线性表存在了操作结果重置为空表
ListEmpty（L）初始条件线性表存在操作结果如果为空表为ture
ListLength（L）初始条件线性表存在操作结果返回L中数据元素个数
GetElem（L，i，&e）初始太久存在操作结果用e返回L中第i哥元素值
LocateElem（L，e，compare（））初始线性表存在，compare是数据元素判定函数操作结果返回L中第一个与e满足compare的数据元素的位序若这样的数据元素不存在返回0
PriorElem(L,cur_e,&pre_e)初始为L存在操作结果cur_e为L的元素，不是第一个，则pre_e返回他的前驱，否则操作失败 pre_e没有意义
NextElem(L,cur_e,&next_e)初始L存在，如果cur存在返回后继
Listinsert（&L，i，e）L存在 L在第i个位置之前插入新的元素e，L的长度加1
ListDelete（&L，i，&e）L存在删除L的第i个元素，用e返回，L减一。
ListTraversr（&L，visited（））L存在操作结果依次对线性表中每个元素调用visited（）

3.线性表的顺序表示和实现

//顺序表的类型定义
typedef struct{
    ElemType data[];//*data为动态分配
    int length;
}SqList;
//
SqList L;
L.data=(ElemType*)malloc(sizeof(ElemTAype)*M)
//



//
#define  LIST_INTI_SIZE 100
typedef	struct {
	int elem[LIST_INTI_SIZE];
	int length;
}Sqlist;

//多项式的顺序存储结构类型定义
#define MAXSIZE 1000//最大长度
typedef struct {
	float p;
	int e;
}Polynomial;
typedef struct {
	Polynomial* elem;//存储基地址//数组
	int length;//当前的项个数
}SqList;

//图书表的顺序存储
#define MAXSIZE 1000
typedef struct {
	char no[20];
	char name[50];
	float price;
}book;
typedef struct {
	book* elem;
	int length;
}SqList;

#include "stdio.h"    
#include "stdlib.h"  
#include "math.h"  
#include "time.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
//#define OVERFLOW -2
#define INFEASIBLE -1
#define MAXSIZE 20   
typedef char ElemType;
typedef int Status;
typedef struct
{
	ElemType *elem;
	int length;
}SqList;
//1.线性表的初始化
Status InitList_Sq(SqList* L)
{
	//分配空间
	L->elem = (ElemType*)malloc(sizeof(ElemType) * MAXSIZE);
	//L->elem = new ElemType[MAXSIZE]; C++写法
	if (!L->elem)exit(OVERFLOW);//分配失败
	L->length = 0; return OK;//空表长度为零
}
//2.摧毁线性表L
void DestroyList(SqList* L)
{
	if (L->elem)
		free(L->elem);//delete L->elem;释放空间
}
//3.清空线性表
void ClearList(SqList* L)
{
	L->length = 0;//将线性表长度为0
}
int GetLength(SqList* L)
{
	return (L->length);
}
//4判断线性表为空
int IsEmpty(SqList L)
{
	if (L.length == 0) return 1;
	else return 0;
}
//5顺序表的取值
int GetElem(SqList L, int i, ElemType& e)
{
	if (i<1 || i>L.length) return ERROR;
	e = L.elem[i - 1]; return OK;
}
//6插入
Status Listlnsert_Sq(SqList* L, int i, ElemType e)
{
	int j; if (i<1 || i>L->length + 1)return ERROR;
	if (L->length == MAXSIZE) return ERROR;
	for (j = L->length; j >= i - 1; j--)
		L->elem[j+1] = L->elem[j];
	L->elem[i - 1] = e; L->length++;
	return OK;
}
//7删除
Status ListDelete_Sq(SqList* L, int i)
{
	int j;
	if (i<1 || i>L->length) return ERROR;
	for (j = i; j <= L->length; j++)
		L->elem[j - 1] = L->elem[j];
	L->length--; return OK;
}
int main()
{
	SqList L;
	InitList_Sq(&L);
	GetLength(&L);
}

优点

存储量大可以随机读取表中的元素

缺点

增删要移动大量元素浪费存储空间静态

4线性表的链式

结点：数据元素的存储映像。由数据域和指针域
链表：N个结点由指针域组成链表它是线性表的链式存储映像名称为线性表的链性存储

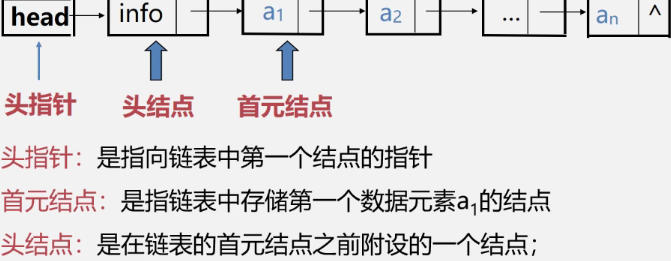
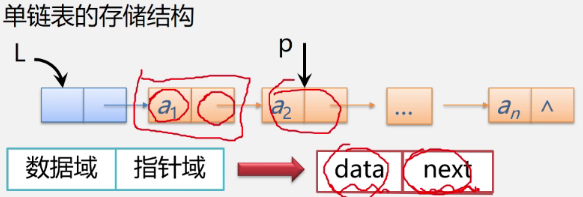
1.单链表

结点只有一个指针域的链表

特点

结点在存储器的位置是任意的，即逻辑上相邻的数据元素，在物理上不一定
访问时只能通过头指针进入链表，并通过每个结点的指针域依次向后，寻找第一个和最后一个结点

栈与队列

栈与队列是两个常用的

栈与队列是限定插入和删除只能在表的端点进行的线性表

1 2	Insert(S,n+1,x) Delete(S,n) Insert(Q,n+1,x) Delete(Q,1)

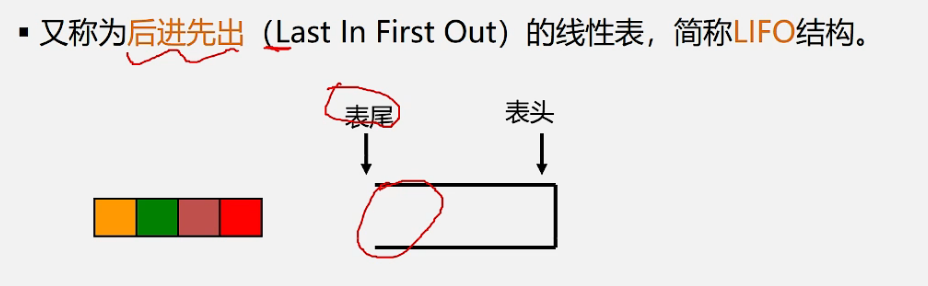
栈–后进先出

使得栈成为有用的工具，数据转换，表达式，函数调用，递归，括号

2队列–先进先出

解决排队问题脱机打印多用户系统等

栈stack

特殊的线性表，是限定在一段，通常是表尾，进行插入和删除操作的线性表

栈的定义

定义：限定在表的一端进行插入和删除的运算线性表
逻辑结构：通线性表一对一的关系
存储结构：顺序表更常见
只能在栈顶运算
入栈和出栈函数

案例

进制转换

十进制N想其他进制数d（二八十六）

**法则为：**除以d倒取余

n=（n div d）*d + n mod d

div为整除运算 mod为求余

例子十进制159转八进制

159/8=19...7
19/8=2...3
2/8=0..2
（237）8

括号匹配的验证

表达式求值

操作数和运算符和界限符

为了实现表达式求值设置两个栈

OPTR寄存运算符操作数栈OPND用于寄存运算数和运算结果

栈的表示和操作

ADK Stack{
数据对象D={ai|ai属于ElemSet}
数据关系R1={<ai-1,ai>}
an端为栈顶，a1为栈底
初始化 进栈出栈 取栈顶等

}ADT Stack

InitStack(&S)初始化操作 构造一个空栈S
DestoryStack(&S) 销毁栈操作
初始条件S存在，结果销毁

StackEmpty 判断是否为空
S存在 空true 否为false

StackLength(S)求栈的长度
S存在 返回S的个数，即栈长度

GetTop(S,&e)去栈顶
S存在且为空
用e返回S的栈顶元素

ClearStack清空

Push(&S,e)入栈

顺序栈的实现，同一般线性表的顺序存完全相同

#define MAXSIZE 100
typedef struct{
    SElemType *base;
    SElemType *top;
    int stacksize
}Sqstack;

初始化

Status InitStack(SqStack &S){
    S.base=(SElemType*)malloc(MAXSIZE*sizeof(SElemType));
    if(!S.base)exiu(OBERFLOW);
    S.top=S.base;
    S.stacksize=MAXSIZE;
    return OK;
}

判断是否为空

Status StackEmpty(SqStack S){
	if(S.top==S.base)return TRUE;
    else return FALSE;

}

顺序栈长度

1
2
3

int StackLength(SqStack S){
return S.top-S.base;
}

清空

Status ClearStack(Sqstack &S){
if(S.base)S,top=S.base;
return OK;
}

销毁

Status DestroyStack(Sqstack &S){
    if(S.base){
        delete S.base;
        S.stacksize=;
        S.base=S.top=NULL;
    }
    return OK;
}

入栈

Status Push (SqStack &S,SElemType e){
    if(S.top-S.base==S.stacksize)return ERROR;
    *S.top=e;
    S.top++;
    return OK;
}

出栈

Status Ppo(SqStack &S,SElemType&e){
	if(S.top==S.base)return ERROEL;
    E=*--s.TOP;
    return OK;
}

链栈

typedef struct StackNode{
    SElemType data;
    struct StackNode *next;
}StackNode,*LinkStack;

LinkStack S;

链表的初始化

void InitStack(LinkStack &S){
    S=NULL;
    return ok;
}

入栈

Status Push(LinkStack &S,SElemType e){
    p=new stacknoode;
    p->data=e;
    p->newt=S;
    S=p;
    return OK;
}

出栈

Status Pop(LinkStack&S,SElemTyoe &e){
    if(S==NULL)return ERROE;
    e=s->data;
    p=S;
    S=S->next;
    delete p;
    
}

栈与递归

递归定义的函数递归数据结构递归解法

队列queue

先进先出FiFO

表一插入，在另一端表头删除

队列的相关概念

定义头删尾插
逻辑结构一对一先信标
循环和链队
之恶能在对手和队尾
入和出队

树

树的定义

Tree是由包括零，多个结点的有限集，分为空树
�限集，分为空树